简单介绍图及其相关算法。
1. 什么是图
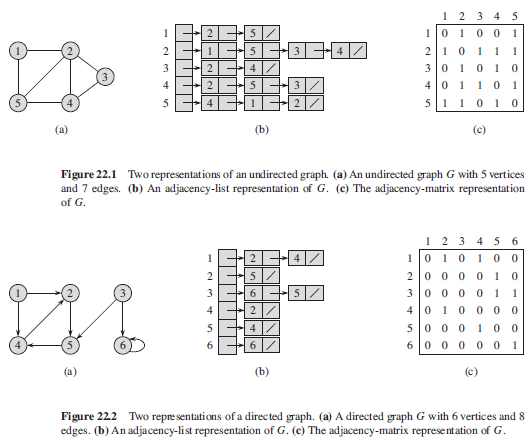
定义 一个图 $G = (V, E)$ 由顶点(或结点)的非空集 $V$ 和边的集合 $E$ 构成,每条边有一个或两个顶点与它相连,这样的顶点称为边的端点。边连接它的端点。
1.1. 图的表示
- 邻接链表:稀疏图
- 邻接矩阵:稠密图,或者需要快速判断任意两个结点之间是否有边的情况
2. 广度优先搜索
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
/** u.color 存放结点 u 的颜色属性
* 白色表示未被发现
* 灰色表示邻接结点中还有白色结点
* 黑色表示邻接结点均被发现
* u.π 存放前驱结点
* u.d 存放从源结点 s 到结点 u 之间的距离
**/
BFS(G, s)
for each vertex u in G.V - {s}
u.color = WHITE
u.d = ∞
u.π = NIL
s.color = BLACK
s.d = 0
s.π = NIL
Q = ∅
ENQUEUE(Q, s)
while Q ≠ ∅ // 灰色结点的集合
u = DEQUEUE(Q)
for each v in G.Adj[u]
if v.color == WHITE
v.color = GRAY
v.d = u.d + 1
v.π = u
ENQUEUE(Q, v)
u.color = BLACK
|
BFS 的总运行时间为 O(V + E)
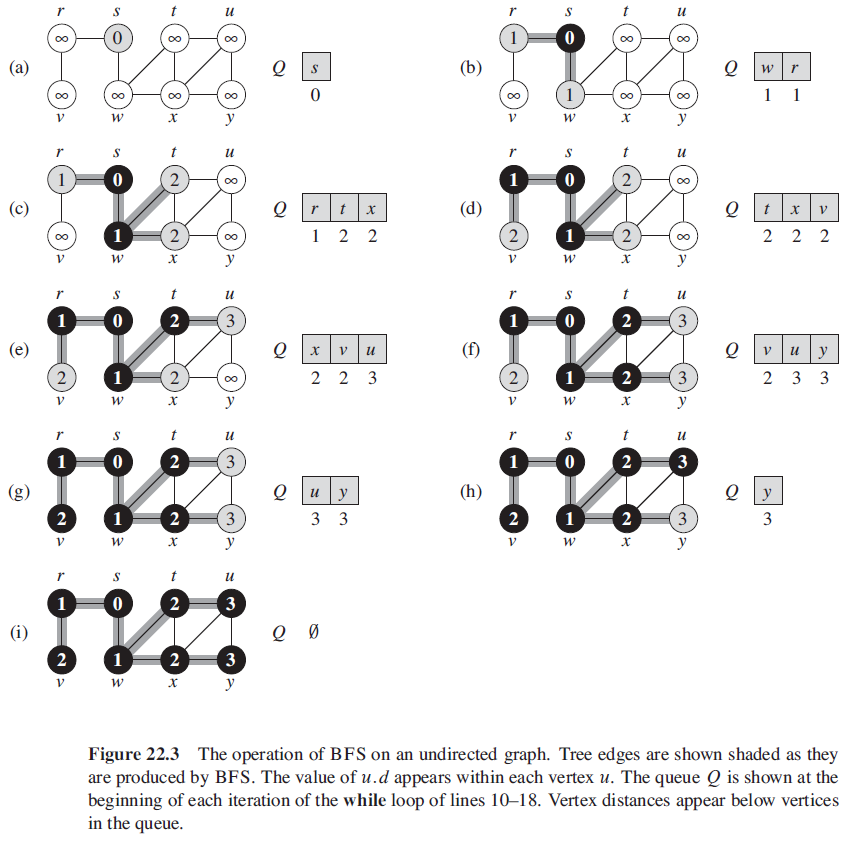
2.1. BFS 的性质
- BFS 可以计算出从源结点 s 到 结点 v 的最短路径。
- BFS 在对图进行搜索的过程中将创建一棵广度优先树
3. 深度优先搜索
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
/** u.color 存放结点 u 的颜色属性
* 白色表示未被发现
* 灰色表示邻接结点中还有白色结点
* 黑色表示邻接结点均被发现
* u.π 存放前驱结点
* u.d 记录结点 u 第一次被发现的时间
* u.f 记录搜索完成对 u 的邻接链表扫描的事件
**/
DFS(G)
for each vertex u in G.V
u.color = WHITE
u.π = NIL
time = 0
for each vertex u in G.V
if u.color == WHITE
DFS-VISIT(G, u)
DFS-VISIT(G, u)
time = time + 1 // white vertex u has just been discovered
u.d = time
u.color = GRAY
for each v in G.Adj[u] // explore edge (u, v)
if v.color == WHITE
v.π = u
DFS-VISIT(G, v)
u.color = BLACK // blacken u, it is finished
time = time + 1
u.f = time
|
DFS 的总运行时间为 O(V + E)
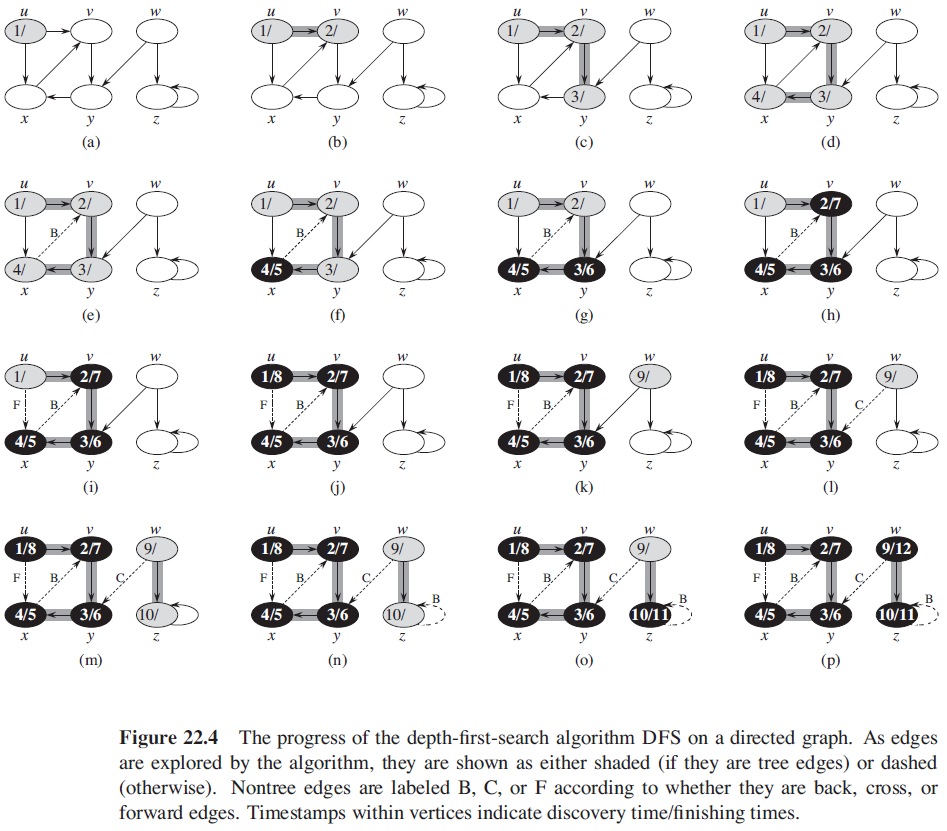
3.1. DFS 的性质
-
括号化定理:在对有向或无向图进行的任意 DFS 中,对于任意两个结点 u 和 v 来说,下面三种情况只有一种成立:
- 区间 $[u.d, u.f]$ 和 区间 $[v.d, v.f$ 完全分离,在深度优先森林中,结点 u 不是结点 v 的后代,结点 v 也不是结点 u 的后代
- 区间 $[u.d, u.f]$ 完全包含在 区间 $[v.d, v.f$ 内,在深度优先树中,结点 u 是结点 v 的后代
- 区间 $[v.d, v.f]$ 完全包含在 区间 $[u.d, u.f$ 内,在深度优先树中,结点 v 是结点 u 的后代
-
边的分类
- 树边:是深度优先森林 $G_π$ 中的边。如果结点 v 是因算法对边 (u, v) 的探索而首先被发现,则 (u, v) 是一条树边
- 后向边:是将结点 u 连接到其在深度优先树中祖先结点 v 的边。由于有向图中可以有自循环,自循环也被认为是后向边
- 前向边:是将结点 u 连接到其在深度优先树中后代结点 v 的边
- 横向边:其他所有的边
在对无向图 G 进行深度优先搜索时,每条边要么是树边,要么是后向边。
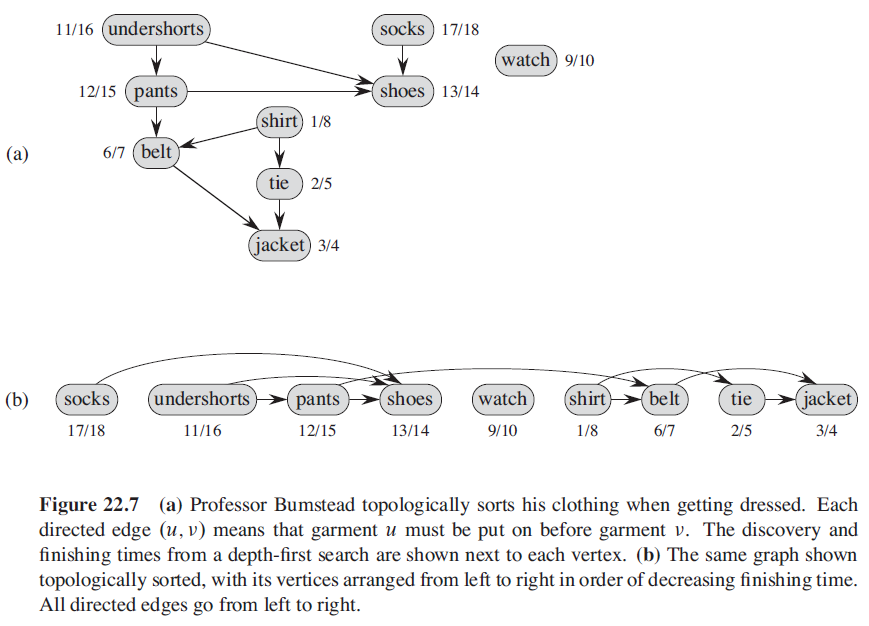
3.2. 拓扑排序
对于一个有向无环图 G(V, E) 来说,其拓扑排序是 G 中所有结点的一种线性次序,该次序满足如下条件:如果图 G 包含边 (u, v),则结点 u 在拓扑排序中处于结点 v 的前面。
1
2
3
4
|
TOPOLOGICAL-SORT(G)
call DFS(G) to compute finishing time v.f for each vertex v
as each vertex is finished, insert it onto the front of a linked list
return the linked of list of vertices
|
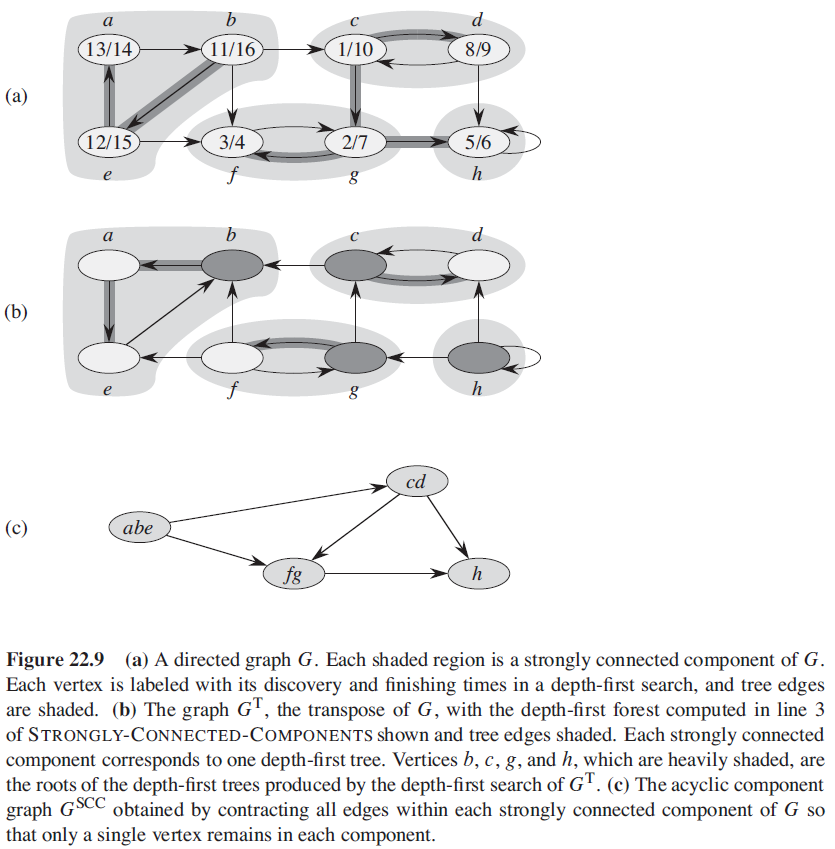
3.3. 强连通分量
定义: 如果一个有向图中任意两个顶点互相可达,则该有向图是强连通的。
图 G 的转置 $G^T = (V, E^T)$,其中 $E^T = {(u, v): (u, v) \in E}$。
1
2
3
4
5
6
7
|
STRONGLY-CONNECTED-COMPONENTS(G)
call DFS(G) to compute finishing time u.f for each vertex u
compute G^T
call DFS(G^T), but in the main loop of DFS, consider the vertices
in order of decreasing u.f (as computed in line 1)
output the vertices of each tree in the depth-first forest formed
in line 3 as a separate strongly connected component
|
4. 最小生成树
定义: 连通加权图里的最小生成树是具有边的权值之和最小的生成树。
1
2
3
4
5
6
7
8
|
// 在每遍循环之前,A 是某棵最小生成树的一个子集
// 加入集合 A 而不会破坏 A 的循环不变式的边称为集合 A 的安全边
GENERIC-MST(G, w)
A = ∅
while A does not form a spanning tree
find an edge(u, v) that is safe for A
A = A ∪ {(u, v)}
return A
|
定理: 设 G = (V, E) 是一个在边 E 上定义了实数值权重函数 w 的连通无向图。设集合 A 为 E 的一个子集,且 A 包括在图 G 的某棵最小生成树中,设 (S, V - S) 是图 G 中尊重集合 A 的任意一个切割(集合 A 中不存在横跨该切割的边),又设 (u, v) 是横跨切割 (S, V - S) 的一条轻边。那么边 (u, v) 对于集合 A 是安全的。
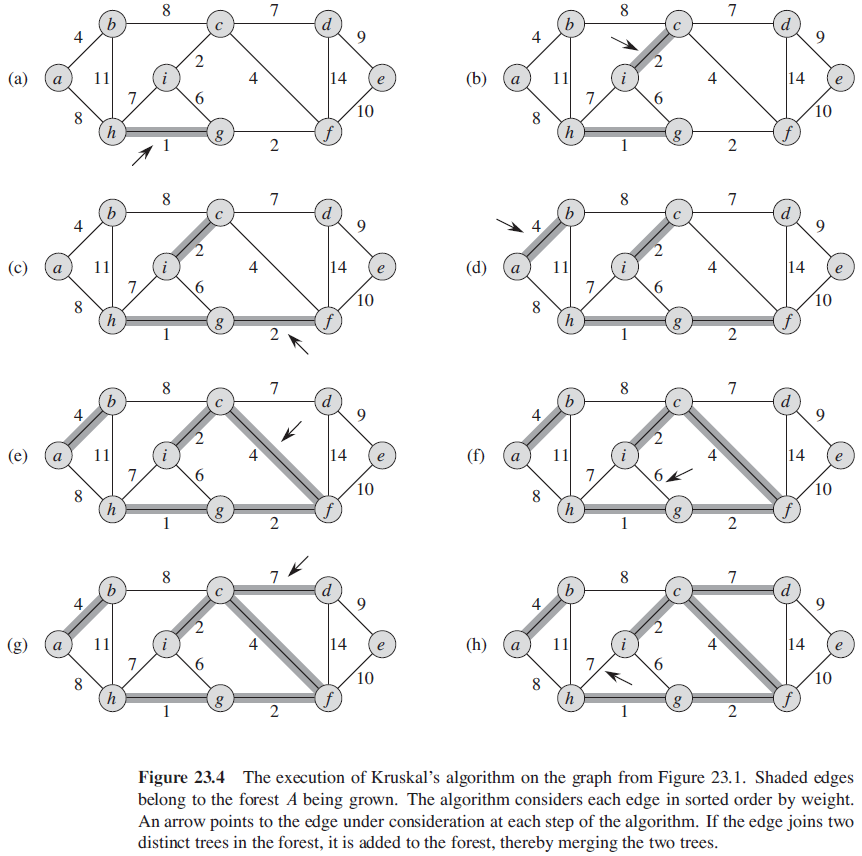
4.1. Kruskal 算法
在 Kurskal 算法中,集合 A 是一个森林,其结点就是给定图的结点。每次加入集合 A 中的安全边永远是权重最小的连接两个不同分量的边。
1
2
3
4
5
6
7
8
9
10
|
MST-KRUSKAL(G, w)
A = ∅
for each vertex v in G.V
MAKE-SET(v)
sort the edge of G.E into nondecreasing order by weight w
for each edge (u, v) in G.E, taken in nondecreasing order by weight
if FIND-SET(u) ≠ FIND-SET(v)
A = A ∪ {(u, v)}
UNION(u, v)
return A
|
Kruskal 算法的时间复杂度为 $O(ElgV)$。
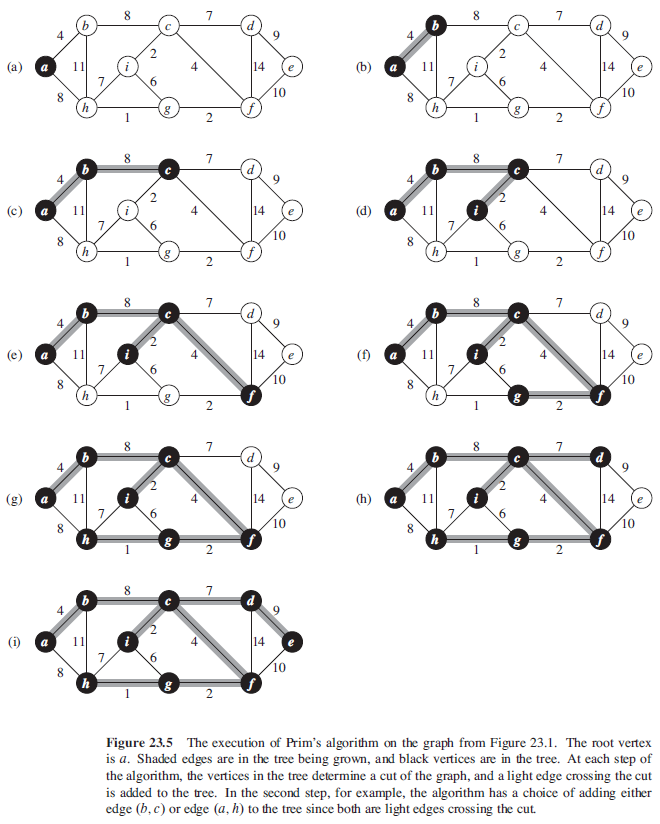
4.2. Prim 算法
在 Prim 算法里,集合 A 则是一棵树。这棵树从一个任意的根结点 r 开始,一直长大到覆盖 V 中的所有结点时为止。每次加入到 A 中的安全边永远是连接 A 和 A 之外某个结点的边中权重最小的边。
1
2
3
4
5
6
7
8
9
10
11
12
|
MST-PRIM(G, w, r)
for each u in G.V
u.key = ∞
u.π = NIL
r.key = 0
Q = G.V
while Q ≠ ∅
u = EXTRACT-MIN(Q)
for each v in G.Adj[u]
if v in Q and w(u, v) < v.key
v.π = u
v.key = w(u, v)
|
如果使用二叉最小优先队列来实现最小优先队列 Q,时间复杂度为 $O(ElgV)$;
如果使用斐波那契堆来实现最小优先队列 Q,则 Prim 算法的运行时间将改进到 $O(E + VlgV)$
5. 单源最短路径
- 最短路径的子路径也是最短路径
- 如果从结点 s 到结点 v 的某条路径上存在权重为负值的环路,我们定义 $\delta(s, v) = -\infty$
- 一般地,我们假定在找到的最短路径中没有环路,即它们都是简单路径。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
/** 初始化
* v.d:s 到 v 的最短路径估计
* v.π:前驱结点 */
INITIALIZE-SINGLE-SOURCE(G, s)
for each vertex v in G.V
v.d = ∞
v.π = NIL
s.d = 0
// 松弛操作
RELAX(u, v, w)
if v.d > u.d + w(u, v)
v.d = u.d + w(u, v)
v.π = u
|
Dijkstra 算法和用于有向无环图的最短路径算法对每条边仅松弛一次。 Bellman-Ford 算法则对每条边松弛 |V| - 1 次。
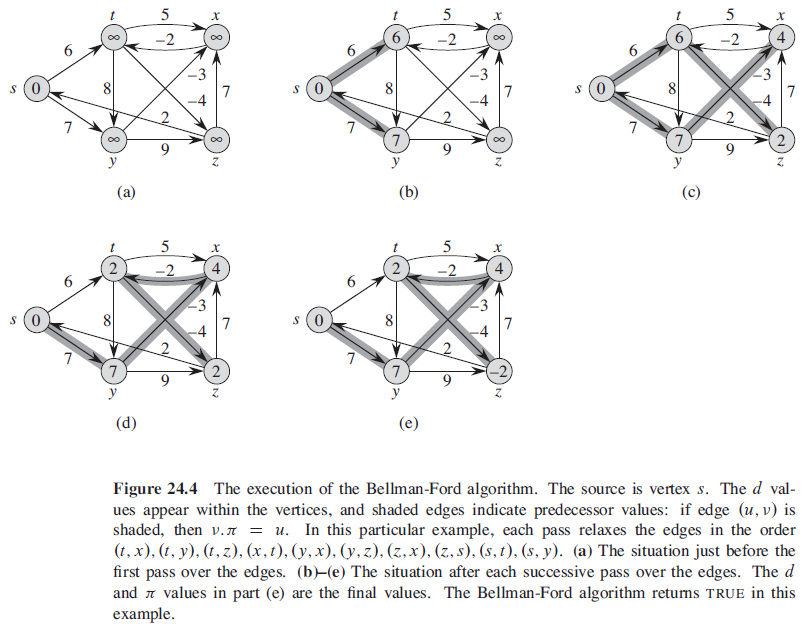
5.1. Bellman-Ford 算法
Bellman-Ford 算法解决的是一般情况下的最短路径问题。该算法返回 TRUE 值当且仅当输入图不包含可以从源结点到达的权重为负值的环路。
1
2
3
4
5
6
7
8
9
|
BELLMAN-FORD(G, w, s)
INITIALIZE-SINGLE-SOURCE(G, s)
for i = 1 to |G.V|-1
for each edge (u, v) in G.E
RELAX(u, v, w)
for each edge (u, v) in G.E
if v.d > u.d + w(u, v)
return FALSE
return TRUE
|
Bellman-Ford 算法的总运行时间为 O(VE)
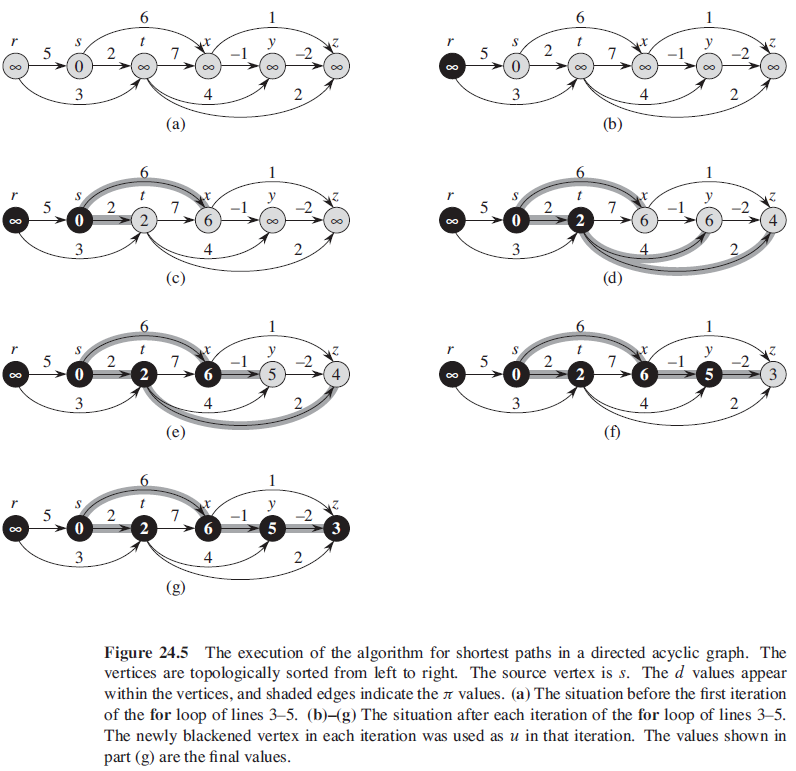
5.2. 有向无环图中的单源最短路径问题
根据结点的拓扑排序次序来对带权重的有向无环图 G = (V, E) 进行边的松弛操作,我们便可以在 $O(V + E)$ 时间内计算出从单个源结点到所有结点之间的最短路径。
1
2
3
4
5
6
|
DAG-SHOPTEST-PATHS(G, w, s)
topologically sort the vertice of G
INITIALIZE-SINGLE-SOURCE(G, s)
for each vertex u, taken in topologically sorted order
for each vertex v in G.Adj[u]
RELAX(u, v, w)
|
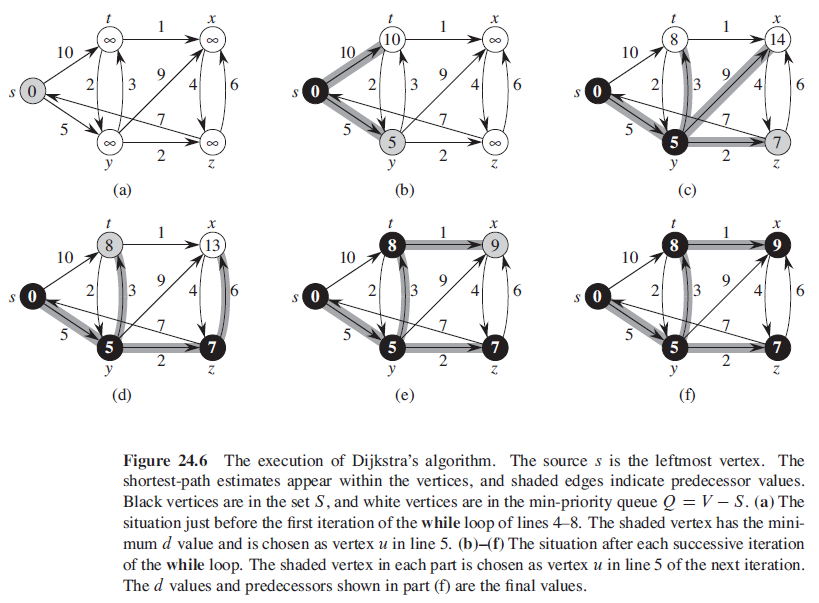
6. Dijkstra 算法
Dijkstra 算法解决的是带权重的有向图上的单源最短路径问题,该算法要求所有边的权重都为非负值。
1
2
3
4
5
6
7
8
9
|
DIJKSTRA(G, w, s)
INITIALIZE-SINGLE-SOURCE(G, s)
S = ∅
Q = G.V
while Q ≠ ∅
u = EXTRACT-MIN(Q)
S = S ∪ {u}
for each vertex v in G.Adj[u]
RELAX(u, v, w)
|
如果使用二叉最小优先队列来实现最小优先队列 Q,时间复杂度为 $O(ElgV)$;
如果使用斐波那契堆来实现最小优先队列 Q,则 Dijkstra 算法的运行时间将改进到 $O(E + VlgV)$