树 - HTT - ふわふわ時間

主要介绍二叉树和红黑树。

1. 什么是树

定义 1 树是没有简单回路的连通无向图。

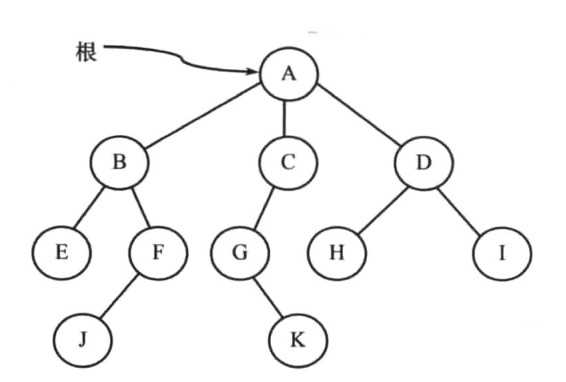
定义 2 有根树是指定一个顶点作为根并且每条边的方向都离开根的树。

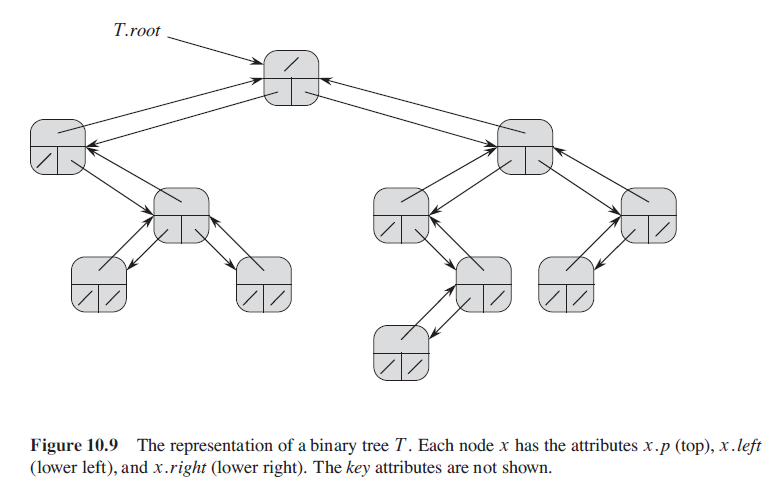
1.1. 二叉树

如果 $x.p = NIL$，则 $x$ 是根结点
属性 $T.root$ 指向整棵树 $T$ 的根结点，如果 $T.root = NIL$，则该数为空

二叉树

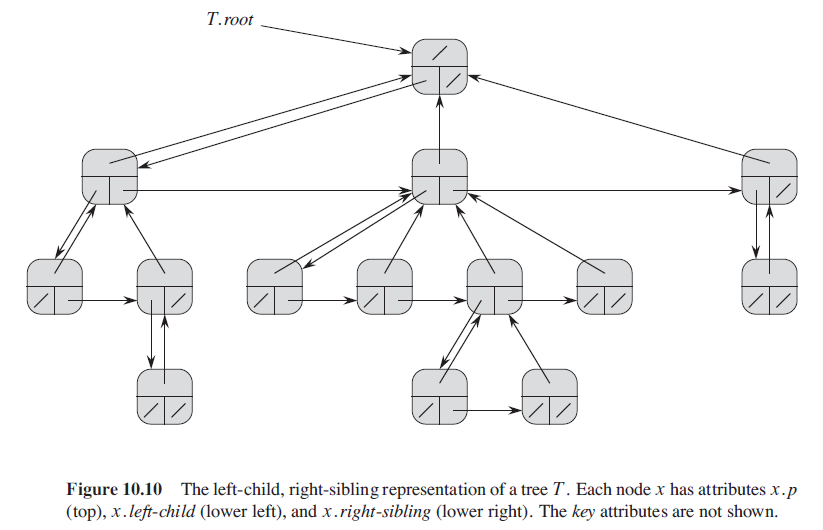
1.2. 分支无限制的有根树

$x.left-child$ 指向结点 $x$ 的最左边的孩子结点
$x.right-sibling$ 指向结点 $x$ 右侧相邻的兄弟结点

分支无限制

2. 二叉搜索树

2.1. 什么是二叉搜索树

二叉搜索树（binary-search-tree，BST）性质：设 $x$ 是二叉搜索树中的一个结点。如果 $y$ 是 $x$ 左子树中的一个结点，那么 $y.key \leq x.key$；如果 $y$ 是 $x$ 右子树中的一个结点，那么 $y.key \geq x.key$。

中序遍历：

1
2
3
4
5


INORDER-TREE-WALK(x)
    if x ≠ NIL
        INOREDER-TREE-WALK(x.left)
        print x.key
        INOREDER-TREE-WALK(x.right)

中序遍历时间复杂度为 O(n)，使用替换法，通过证明 $T(n) \le (c+d)n + c$，可以证得 $T(n) = O(n)$

2.2. 查询二叉搜索树

2.2.1. 查找

递归版本

1
2
3
4
5
6


TREE-SEARCH(x, k)
    if x == NIL or k == x.key
        return x
    if k < x.key
        return TREE-SEARCH(x.left, k)
    else return TREE-SEARCH(x.right, k)

迭代版本（效率更高）

1
2
3
4
5
6


ITERATIVE-TREE-SEARCH(x, k)
    while x ≠ NIL and k ≠ x.key
        if k < x.key
           x = x.left
        else x = x.right
    return x

2.2.2. 最大（小）关键字元素

最小关键字

1
2
3
4


TREE-MINIMUM(x)
    while x.left ≠ NIL
        x = x.left
    return x

最大关键字

1
2
3
4


TREE-MAXIMUM(x)
    while x.right ≠ NIL
        x = .right
    return x

2.2.3. 后继和前驱

如果所有的关键字互不相同，则一个结点 $x$ 的后继是大于 $x.key$ 的最小关键字的结点。二叉搜索树的性质允许我们没有任何关键字的比较来确定一个结点的后继。

1
2
3
4
5
6
7
8


TREE-SUCCESSOR(x)
    if x.right ≠ NIL
        return TREE-MINIMUM(x.right)
    y = x.p
    while y ≠ NIL and x == y.right
        x = y
        y = y.p
    return y

在一棵高度为 $h$ 的二叉搜索树上，动态集合上的操作 SEARCH、MINIMUM、MAXIMUM、SUCCESSOR、PREDECESSOR 可以在 $O(h)$ 时间内完成。

2.3. 插入和删除

2.3.1. 插入

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


TREE-INSERT(T, z)
    y = NIL        // 保存 z 要插入的位置
    x = T.root
    while x ≠ NIL
        y = x
        if z.key < x.key
            x = x.left
        else x = x.right
    z.p = y
    if y == NIL
        T.root = z    // tree T was empty
    else if z.key < y.key
        y.left = z
    else y.right = z

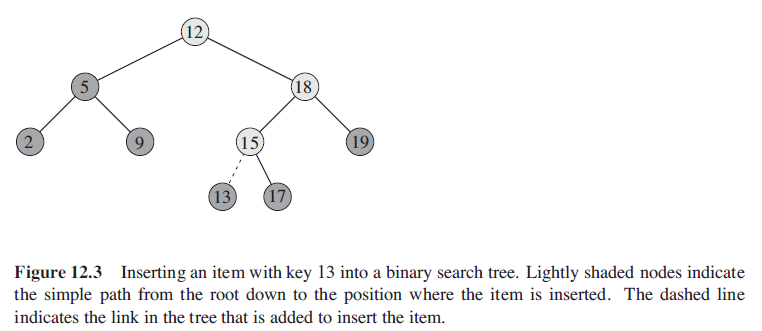
2.3.2. 删除

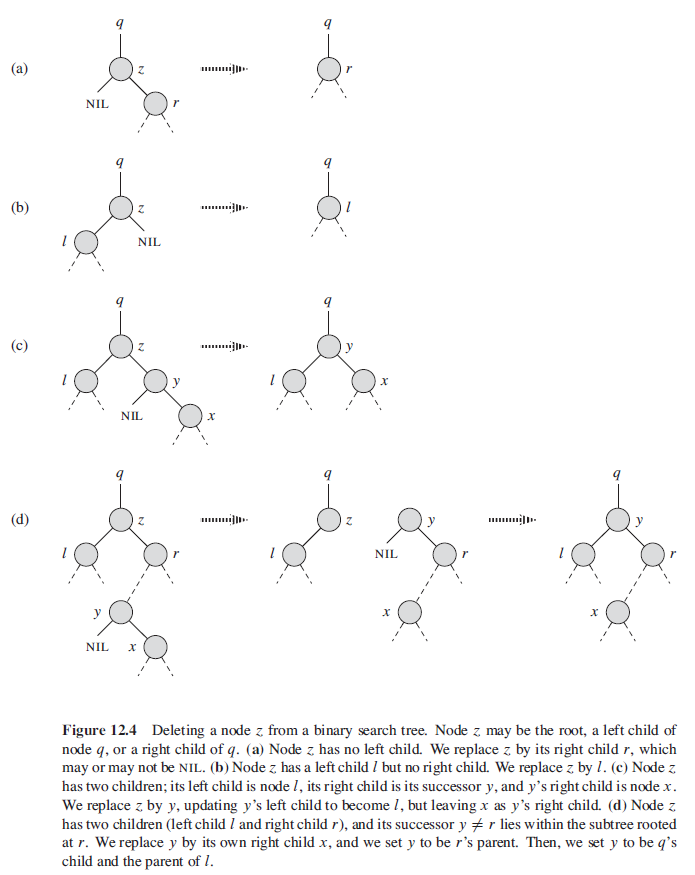
从二叉搜索树 $T$ 中删除结点 $z$ 分为三种基本情况

如果 $z$ 没有孩子结点，那么直接将它删除，并修改它的父结点，用 NIL 替换 $z$
如果 $z$ 只有一个孩子，那么将这个孩子提升到树中 $z$ 的位置上，并修改 $z$ 的父结点，用 $z$ 的孩子来替换 $z$
如果 $z$ 有两个孩子，那么找到 $z$ 的后继 $y$，用 $y$ 来占据树中 $z$ 的位置

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


// 用一棵以 v 为根的子树来替换一棵以 u 为根的子树
TRANSPLANT(T, u, v)
    if u.p == NIL
        T.root = v
    else if u == u.p.left
        u.p.left = v
    else u.p.right = v
    if v ≠ NIL
        v.p = u.p

TREE-DELETE(T, z)
    if z.left == NIL    // (a)
        TRANSPLANT(T, z, z.right)
    else if z.right == NIL    // (b)
        TRANSPLANT(T, z, z.left)
    else y = TREE-MINIMUM(z.right)
        if y.p ≠ z    // (d)
            TRANSPLANT(T, y, y.right)
            y.right = z.right
            y.right.p = y
        TRANSPLANT(T, z, y)    // (c)
        y.left = z.left
        y.left.p = y

在一棵高度为 $h$ 的二叉搜索树上，实现动态集合的操作 INSERT 和 DELETE，可以在 $O(h)$ 时间内完成。一棵有 $n$ 个不同关键字的随机构建二叉搜索树的期望高度为 $O(lg n)$

3. 红黑树

3.1. 红黑树的性质

一棵红黑树是满足下面红黑性质的二叉搜索树：

每个结点或是红色的，或是黑色的
根结点是黑色的
每个叶子结点（NIL）也是黑色的
如果一个结点是红色的，则它的两个子结点都是黑色的
对每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点

从某个结点 $x$ 出发（不含该结点）到达一个叶结点的任意一条简单路径上的黑色结点个数称为该结点的 black-height，记为 bh(x)。

红黑树

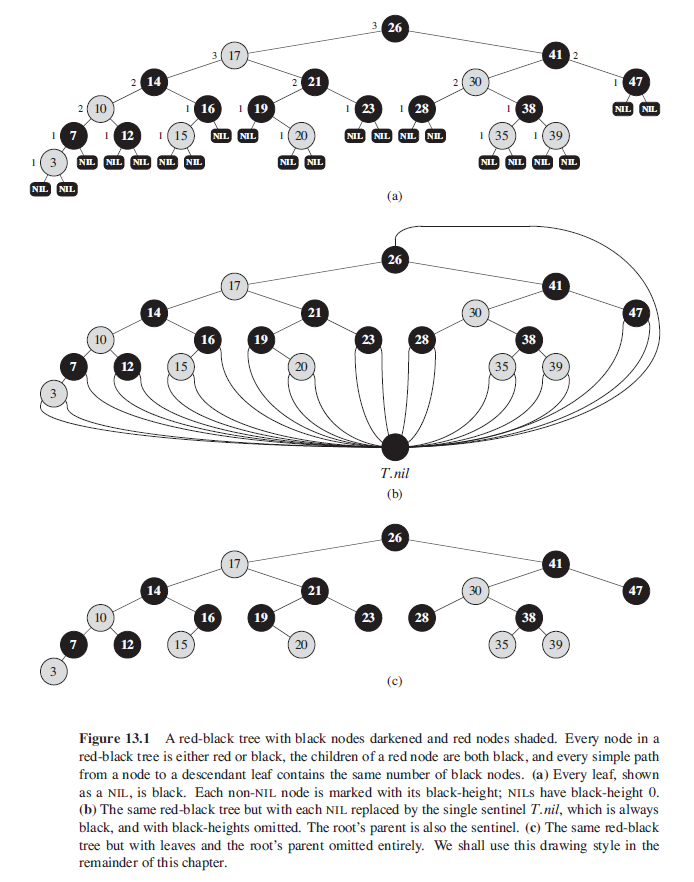
一棵有 $n$ 个内部结点的红黑树的高度至多为 $2lg(n+1)$。

3.2. 旋转

旋转是一种能保持二叉搜索树性质的局部操作。分为两种旋转：左旋和右旋。

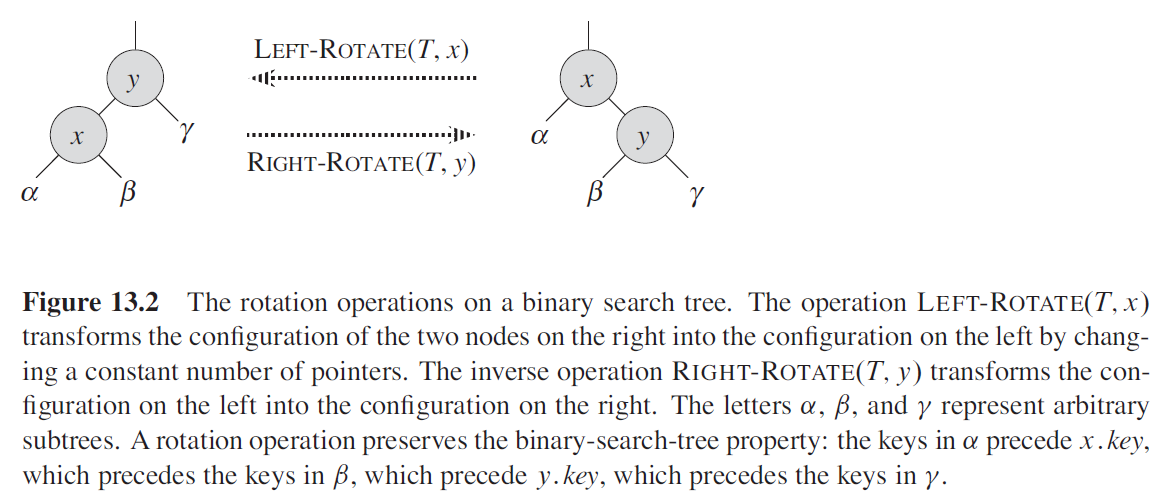
在 LEFT-ROTATION 的伪代码中，假设 $x.right \ne T.nil$ 且根结点的父结点为 $T.nil$。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


LEFT-ROTATION(T, x)
    y = x.right            // set y
    x.right = y = left    // turn y's left subtree into x's right subtree
    if y.left ≠ T.nil
        y.left.p = x
    y.p = x.p            // link x's parent to y
    if x.p == T.nil
        T.root = y
    else if x == x.p.left
        x.p.left =y
    else x.p.right = y
    y.left = x            // put x on y's left
    x.p = y

RIGHT-ROTATION 操作的伪代码是对称的。在旋转操作中只有指针改变，其他属性都保持不变。下图给出了一个 LEFT-ROTATION 操作修改二叉搜索树的例子。

左旋例子

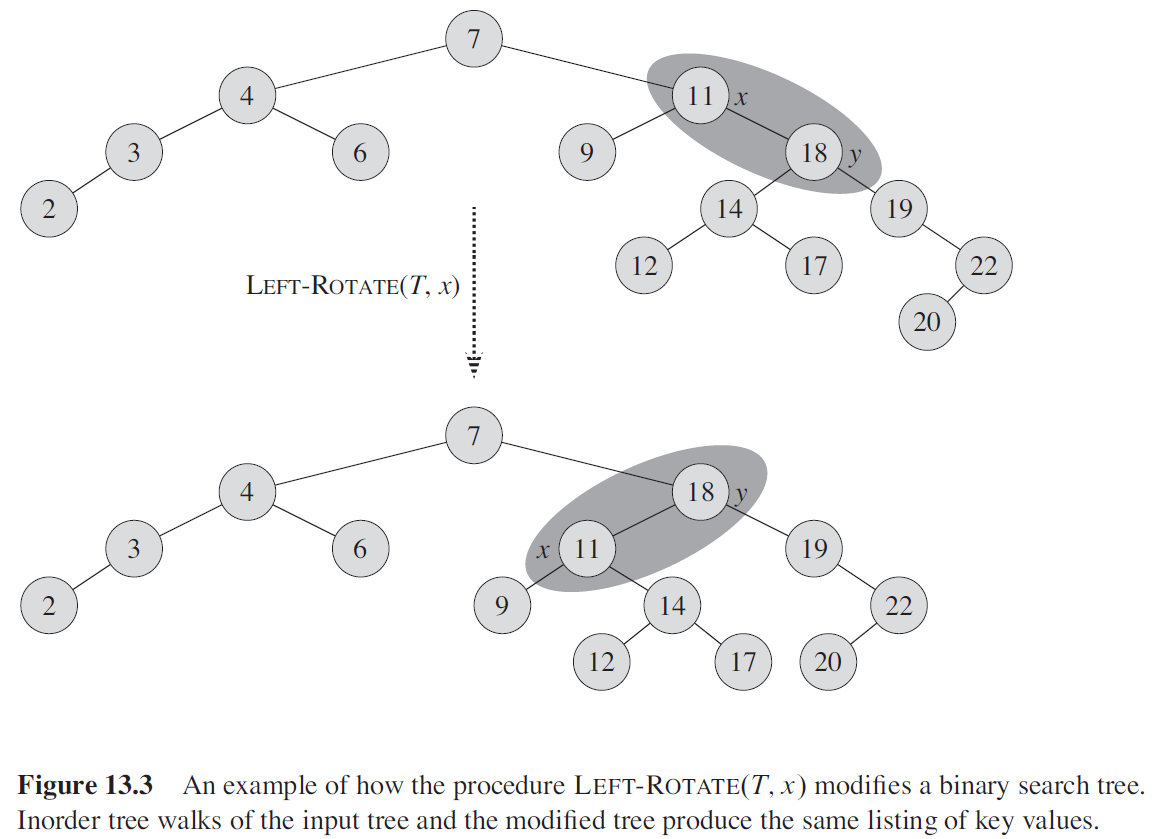
3.3. 插入

有三种情况：

$z$ 的叔结点 $y$ 是红色的
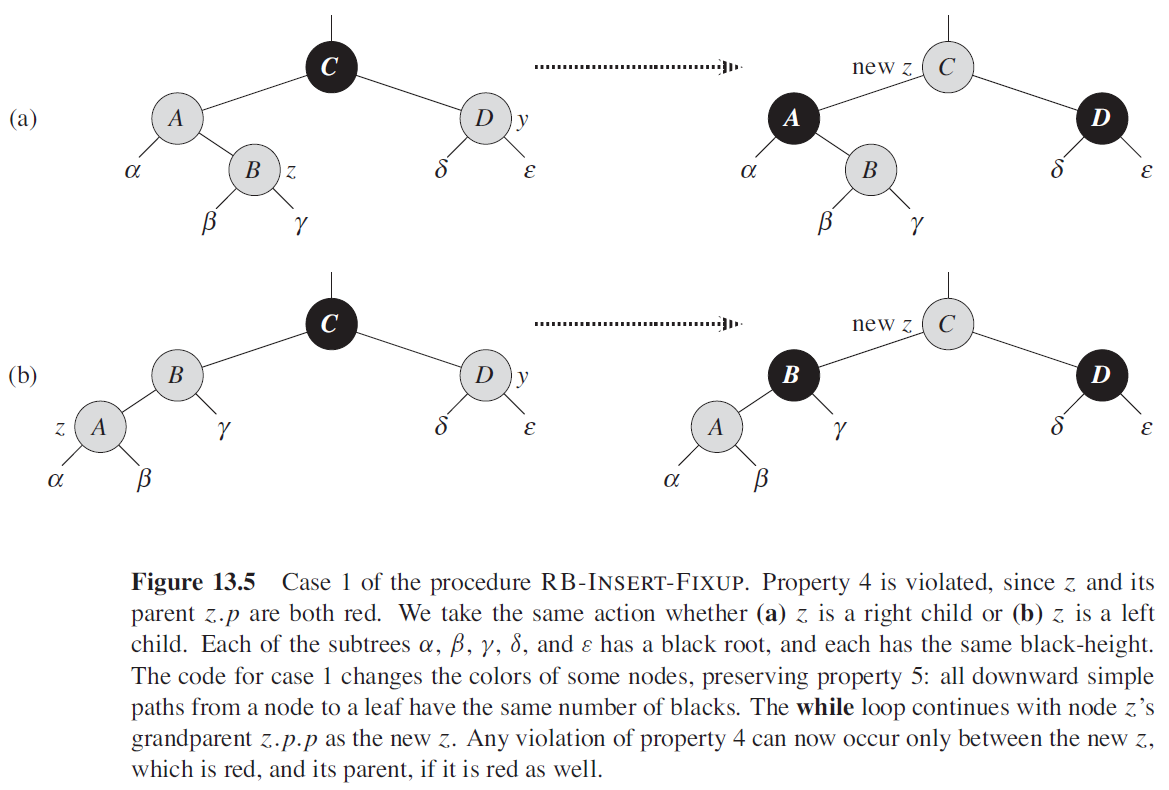
$z$ 的叔结点 $y$ 是黑色的且 $z$ 是一个右孩子
$z$ 的叔结点 $y$ 是黑色的且 $z$ 是一个左孩子

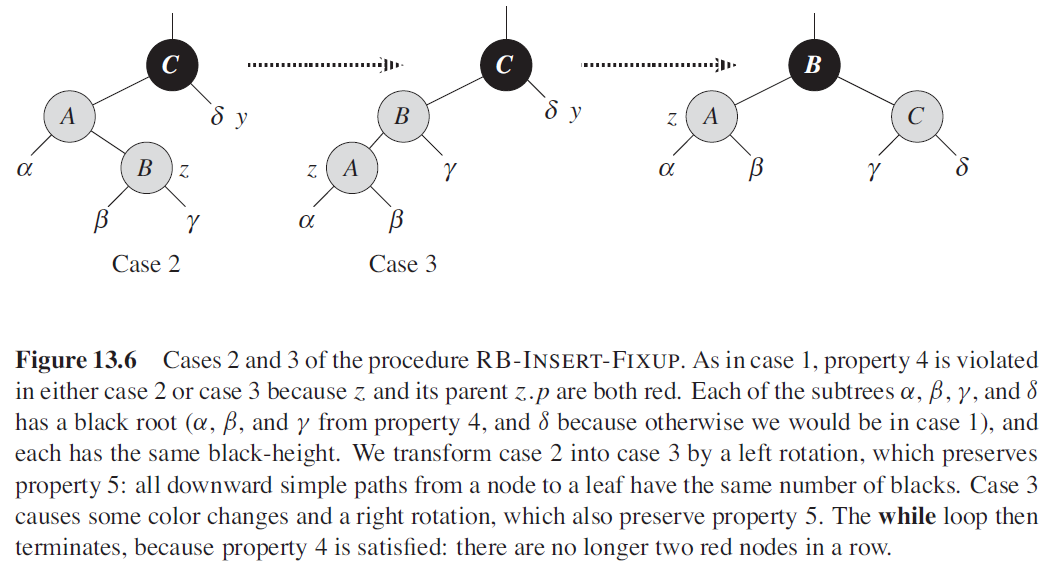
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39


// 将 z 插入树 T 中，然后将 z 着为红色
RB-INSERT(T, z)
    y = T.nil
    x = T.root
    whil x ≠ T.nil
        y = x
        if z.key < x.key
            x = x.left
        else x = x.right
    z.p = y
    if y == T.nil
        T.root = z
    else if z.key < y.key
        y.left = z
    else y.right = z
    z.left = T.nil
    z.right = T.nil
    z.color = RED
    RB-INSERT-FIXUP(T, z)

// 插入 z 后，对树进行调整来保持红黑性质
RB-INSERT-FIXUP(T, z)
    while z.p.color == RED
        if z.p == z.p.p.left
            y = z.p.p.right
            if y.color == RED
                z.p.color = BLACK        // case 1
                y.color = BLACK         // case 1
                z.p.p.color = RED        // case 1
                z = z.p.p                // case 1
            else if z == z.p.right
                z = z.p                    // case 2
                LEFT-ROTATION(T, z)        // case 2
            z.p.color = BLACK            // case 3
            z.p.p.color = RED            // case 3
            RIGHT-ROTATION(T, z.p.p)    // case 3
        else(same as then clause
                with "right" and "left" exchanged)
    T.root.color = BLACK

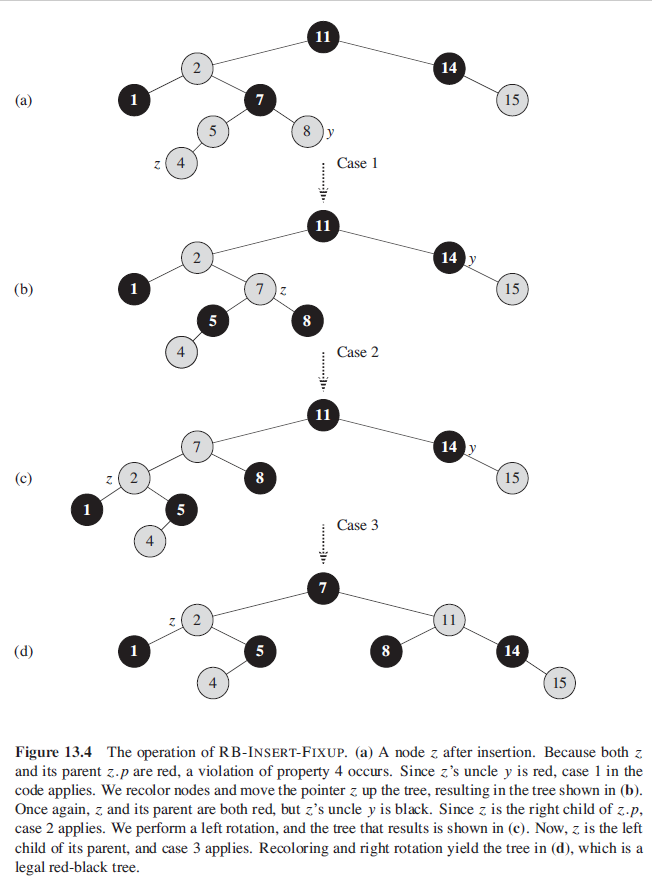
红黑树插入

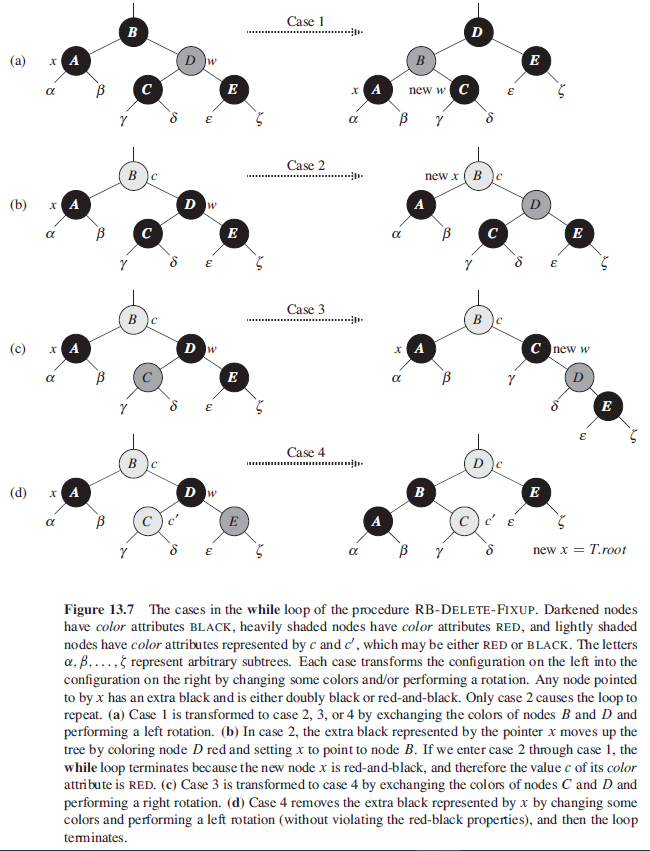
3.4. 删除

有四种情况：

$x$ 的兄弟结点 $w$ 是红色的
$x$ 的兄弟结点 $w$ 是黑色的，而且 $w$ 的两个子结点都是黑色的
$x$ 的兄弟结点 $w$ 是黑色的， $w$ 的左孩子是红色的，右孩子是黑色的
$x$ 的兄弟结点 $w$ 是黑色的，且 $w$ 的右孩子是红色的

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60


// 用一棵以 v 为根的子树来替换一棵以 u 为根的子树
RB-TRANSPLANT(T, u, v)
    if u.p == T.nil
        T.root = v
    else if u == u.p.left
        u.p.left = v
    else u.p.right = v
v.p = u.p

// 过程和 TREE-DELETE 类似
RB-DELETE(T, z)
    y = z
    y-original-color = y.color
    if z.left == T.nil
        x = z.right
        RB-TRANSPLANT(T, z, z.right)
    else if z.right == T.nil
        x = z.left
        RB-TRANSPLANT(T, z, z.left)
    else y = TREE-MINIMUM(z.right)
        y-orginal-color = y.color
        x = y.right
        if y.p == z
            x.p = y
        else RB-TRANSPLANT(T, y, y.right)
            y.right = z.right
            y.right.p = y
        RB-TRANSPLANT(T, z, y)
        y.left = z.left
        y.left.p = y
        y.color = z.color
    if y-orginal-color == BLACK
        RB-DELETE-FIXUP(T, x)

// 通过改变颜色和执行旋转来恢复红黑性质
RB-DELETE-FIXUP(T, x)
    while x ≠ T.root and x.color == BLACK
        if x == x.p.left
            w = x.p.right
            if w.color == RED
                w.color = BLACK            // case 1
                x.p.color = RED            // case 1
                LEFT-ROTATION(T, x.p)    // case 1
                w = x.p.right            // case 1
            if w.left.color == BLACK and w.right.color == BLACK
                w.color = RED            // case 2
                x = x.p                    // case 2
            else if w.right.color == BLACK
                w.left.color = BLACK    // case 3
                w.color = RED            // case 3
                RIGHT-ROTATION(T, w)    // case 3
                w = x.p.right            // case 3
            w.color = x.p.color        // case 4
            x.p.color = BLACK        // case 4
            w.right.color = BLACK    // case 4
            LEFT-ROTATION(T, x.p)    // case 4
            x = T.root                // case 4
        else (same as then clause wiht
                "right" and "left" exchanged)
    x.color = BLACK

四种情况

Table of Contents