《LSM-based Storage Techniques: A Survey》 阅读笔记。
1. LSM-tree Basics
1.1. History of LSM-tree
1.1.1. Update index structure
In general, an index structure can choose one of two strategies to handle updates:
in-placeupdate structure: directly overwrites old records to store new updates (such as $B^+$-tree)- 优点:数据仅保留一份,利于读操作
- 缺点
- 由于随机写入的影响,写操作性能不佳
- 由于更新和删除操作的影响,容易形成碎片,降低磁盘空间利用率
out-of-placeupdate structure: always stores updates into new locations instead of overwriting old entries (such as LSM-tree)- 优点:
- 得益于顺序 IO,写操作性能提升
- 因为无须修改旧数据,因此故障恢复逻辑简单
- 缺点:
- 数据保留多份,读操作性能不佳
- 已废弃数据仍保存在磁盘中,降低磁盘空间利用率
因此需要 compaction,以提升磁盘空间利用率和读操作性能
- 优点:
1.1.2. The original LSM-tree design
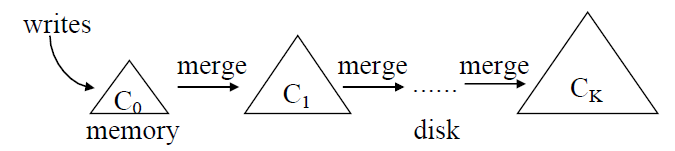
- Contains a sequence of components $C_0, C_1, \cdots, C_k$, each component is structured as a $B^+$-tree
- $C_0$ resides in memory and servers incoming writes, while $C_1, \cdots, C_k$ reside on disk
- When $C_i$ is full, a rolling merge process is triggered to merge of leaf pages from $C_i$ into $C_{i+1}$
Principle: Under a stable workload, where the number of levels remains static, write performance is optimized when the size ratios $T_i = \frac{|C_{i+1}|}{|C_i|}$ between all adjacent components are the same.
1.1.3. Stepped-merge policy
- Similar structure with the original LSM-tree
- Organizes the components into levels, and when level $L$ is full with $T$ components, these $T$ components are merged together into a new component at level $L+1$
1.2. Today$'$s LSM-tree
1.2.1. Basic Structure
-
Apply updates out-of-place to reduce random I/Os
- All incoming writes are appended into a memory component
- An insert or update operation simply adds a new entry
- A delete operations adds an anti-matter entry indicating that a key has been deleted
-
Exploit the immutability of disk components to simplify concurrency control and recovery.
- multiple disk components are merged together into a new one without modifying existing components
-
An LSM-tree component can be implemented using any index structure
- Organize memory components using a concurrent data structure
- skip-list
- $B^+$-tree
- Organize disk components using sorted data structure
- Sorted-String Tables (SST): contains a list of data blocks and an index block
- a data block stores key-value pairs ordered by keys
- an index block stores the key ranges of all data blocks
- $B^+$-tree
- Sorted-String Tables (SST): contains a list of data blocks and an index block
- Organize memory components using a concurrent data structure
-
Query
- A point lookup query, which fetches the value for a specific key, can simply search all components one by one, from newest to oldest, and stop immediately after the first match is found.
- A range query can search all components at the same time, feeding the search results into a priority queue to perform reconciliation.
-
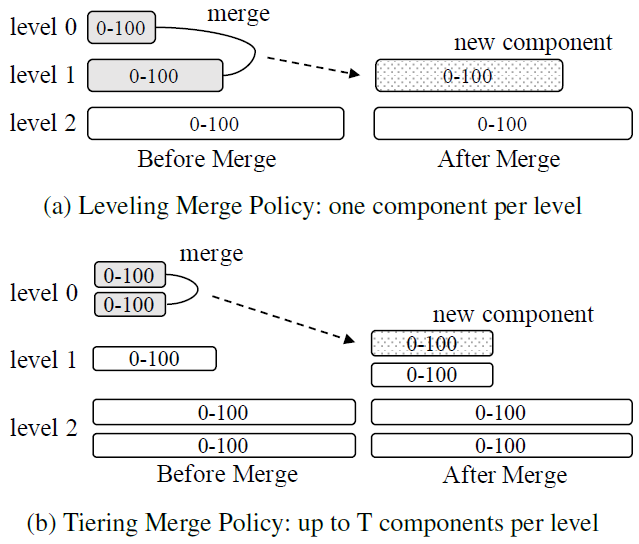
Two types of merge policies
-
leveling mergepolicy (query optimized)- Each level only maintains $1$ component
- The component at level $L$ is $T$ times larger than the component at level $L - 1$
- 优点:components 数量少,query 性能较佳
- 缺点:$L$ 层的 component 在达到本层大小阈值之前,需要和 $L - 1$ 层的 component 合并复数次,写放大较大
写放大 = 磁盘写入的数据量 / 实际的数据量
-
tiering mergepolicy (write optimized)- Maintains up to $T$ components per level (overlapping key ranges)
- When level $L$ is full, its $T$ components are merged together into a new component at level $L + 1$
If level $L$ is already the configured maximum level, then the resulting component remains at level $L$
- 优点:降低 merge 频率,写性能较佳
- 缺点:components 数量多,query 性能稍差
-
1.2.2. Some Well-Known Optimizations
-
Bloom Filter
- improve point lookup performance
- the false positive rate is: $(1 - e^{-\frac{nk}{m}})^k$
- $m$ is the total number of bits
- $n$ is the number of keys
- $k$ is the number of hash functions
- the optimal $k$ that minimizes the false positive rate is $k = \frac{m}{n}\ln{2}$
-
Partitioning
-
partitioning is orthogonal to merge policies, both leveling and tiering (as well as other emerging merge policies) can be adapted to support partitioning.
-
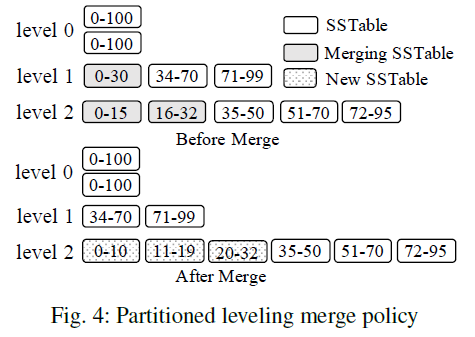
Partitioned leveling merge policy- The disk component at each level(except level 0) is range-partitined into multiple fixed-size SSTables
- To merge an SSTable from level $L$ into level $L + 1$, all of its overlapping SSTables at level $L + 1$ are selected, and these SSTables are merged with it to produce new SSTables still at level $L + 1$
- LevelDB uses a round-robin policy to select which SSTable to merge next at each level
-
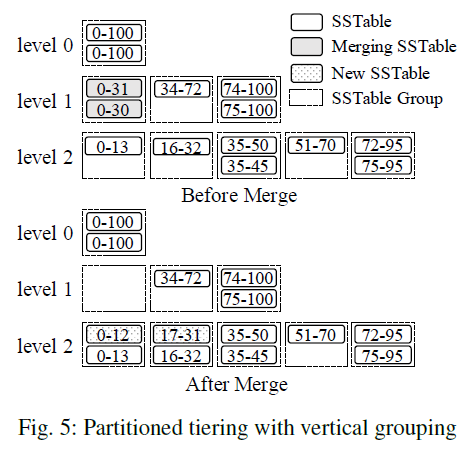
Partitioned tiering with vertical grouping- Overlapping key ranges are grouped together so that the groups have disjoint key ranges
- Merge: all of the SSTables in a group are merged together to produce the resulting SSTables based on the key ranges of the overlapping groups at the next level, which are then added to these overlapping groups
- SSTables are no longer fixed-size since they are produced based on the key ranges of the overlapping groups at the next level
依赖 key 的范围进行分区,因此不同 Group 的 key 范围无重叠,但是 SSTable 的大小不固定
-
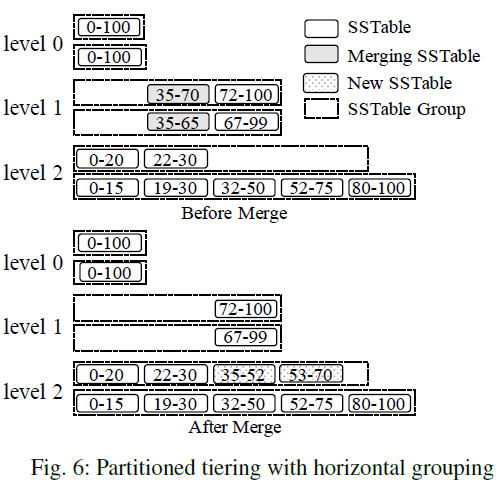
Partitioned tiering with horizontal grouping- Each component is range-partitioned into a set of fixed-size SSTables, serves as logical group directly
- Each level $L$ further maintains an active group to receive new SSTables merged from the previous level
- Merge: selects the SSTables with overlapping key ranges from all of the groups at a level, and the resulting SSTables are added to the active group at the next level
- It is possible one SSTable from a group may overlap a large number of SSTables in the remaining groups
SSTable 大小固定,但是不同 Group 的 key 范围有重叠
-
1.2.3. Concurrency Control and Recovery
-
Concurrency Control
- use a locking scheme or a multi-version scheme
- maintain a reference counter
-
Recovery
- write-ahead logging(WAL)
- a no-steal buffer management policy
- For unpartitioned LSM-trees, adding a pair of timestamps to each disk component
- For partitioned LSM-tress, (LevelDB and RocksDB) maintains a separate metadata log (manifest) to store all changes to the structural metadata, such as adding or deleting SSTables
Tips: Steal vs No-Steal buffer management
Dirty Page: A page with modifications by an uncommitted transaction is a dirty page until either commit or rollback processing for that transaction has been completed.Steal policy: pages can be written out to disk even if the transaction having modified the pages is still activeNo-Steal policy: all dirty pages are retained in the buffer pool until the final outcome of the transaction has been determined
1.3. Cost Analysis
- The cost of writes and queries is measured by counting the number of disk I/Os per operation
Write amplification: measures the overall I/O cost for this entry to be merged into the largest levelSpace amplification: the overall number of entries divided by the number of unique entries
- This analysis considers an unpartitioned LSM-tree and represents a worst-case cost
Levelingis optimized for query performance and space utilization by maintaining one component per level, while with higher write cost by a factor of $T$Tieringis optimized for write performance by maintaining up to $T$ components at each level, while will decrease query performance and worsen space utilization by a factor of $T$
| Merge Policy | Leveling | Tiering |
|---|---|---|
| Write amplification | $O(T \cdot \frac{L}{B})$ | $O(\frac{L}{B})$ |
| Point Lookup (Zero-Result) | $O(L \cdot e^{-\frac{m}{n}})$ | $O(T \cdot L \cdot e^{-\frac{m}{n}})$ |
| Point Lookup (Non-Zero-Result) | $O(1)$ | $O(1)$ |
| Short Range Query | $O(L)$ | $O(T \cdot L)$ |
| Long Range Query | $O(\frac{s}{B})$ | $O(T \cdot \frac{s}{B})$ |
| Space Amplification | $O(\frac{T+1}{T})$ | $O(T)$ |
where,
T: size ratio of a given LSM-treeL: total levelsB: the number of entries that each data page can store- False positive rate: $O(e^{-\frac{m}{n}})$, $m$ bits and $n$ total keys
s: the number of unique keys accessed by a range query- Long Range Query: $\frac{s}{B} > 2 \cdot L$
2. LSM-tree improvements
2.1. Reducing Write Amplification
2.1.1. Tiering
-
WriteBuffer Tree (WB-tree)
- variant of the
partitoned tiering with vertical grouping - relies on hash-partitioning to achieve workload balance so that each SSTable group roughly stores the same amount of data
gives up the ability of supporting range queries
- organizes SSTable groups into a $B^+$-tree-like structure to enable self-balancing to minimize the total number of levels
- variant of the
-
Light-Weight Compaction tree (LWC-tree)
- variant of the
partitoned tiering with vertical grouping - if a group contains too many entries, it will shrink the key range of this group after the group has been merged (now temporarily empty) and will widen the key ranges of its sibling groups accordingly
- variant of the
-
PebblesDB
- variant of the
partitoned tiering with vertical grouping - key ranges of SSTable groups, are selected probabilistically based on inserted keys to achieve workload balance
- performs parallel seeks of SSTables to improve range query performance
- variant of the
-
dCompaction
- variant of the
tiering mergepolicy - introduces the concept of virtual SSTables and virtual merges, delays a merge operation until multiple SSTables can be merged together, reduces the merge frequency
- variant of the
-
SifrDB
- variant of the
partitioned tiering with horizontal grouping - proposes an early-cleaning technique to reduce disk space utilization during merges
- exploits I/O parallelism to speedup query performance by examining multiple SSTables in parallel
- variant of the
2.1.2. Merge Skipping
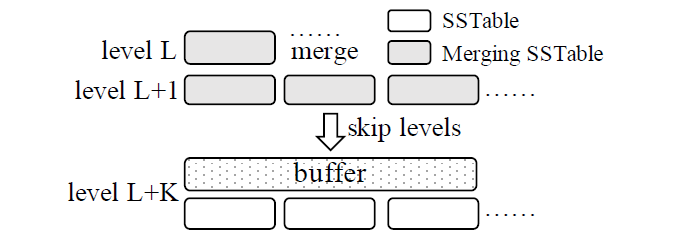
如下图所示,在 skip-tree 中提出:
- 当在 $L$ 层 merge 时,可以将部分 key 直接推送至一个与 $L + K$ 层关联的 buffer
- 只有当 key 不存在于 $L + 1, \dots, L + K - 1$ 层时,才可以直接推送至 $L + K$ 层
- 为保证 buffer 中的数据不丢失,skip-tree 使用了 WAL 机制
- 在随后的 merge 操作时,再将 buffer 中的内容合并入 $L + K$ 层
2.1.3. Exploiting Data Skew
TRIAD 通过采用以下方法降低写放大:
- 区别对待冷热 key
- 只有冷 key 会落盘
- 热 key 虽然不落盘,但是为了清理旧的 binlog,会将热 key 的 log 复制到新的 binlog 中
- 在 level 0 含有多个 SSTables 时再执行 merge
- 当数据落盘时,不生成新的文件,而是直接使用 binlog
- 虽然其在 binlog 中加入了索引以提升点查找性能,但是因为 binlog 无序,因此范围查询性能较差
2.2. Optimizing Merge Operations
2.2.1. Improving Merge Performance
-
VT-tree
- 基本思想:当合并多个 SSTables 时,若某一 SSTable 中的某一 page 和其他 SSTables 中的 pages key 范围均无重叠,则在合并后的 SSTable 中直接指向该 page,减少了读取/拷贝该 page 的消耗
- 衍生问题:
-
Q: 由于 pages 在磁盘上不再是连续地存储着,因此会带来碎片
A: VT-tree 通过设定一个阈值 $K$ (只有连续超过 $K$ 个 pages 无重叠时可免去读取、拷贝过程) 减轻了碎片化
-
Q: 这些 pages 中的 key 在合并时没经历扫描过程,无法设置 Bloom filter
A: VT-tree uses
quotient filterssince multiple quotient filters can be combined directly without accessing the original keys
-
-
Pipelined merge
- 如下图所示,将 merge 过程分成三个阶段,使用流水线式实现,从而更好地利用 CPU 和 I/O 并行来提高合并性能
read phase: reads pages from input SSTables (I/O heavy)merge-sort phase: produce new pages (CPU heavy)write phase: writes the new pages to disk (I/O heavy)
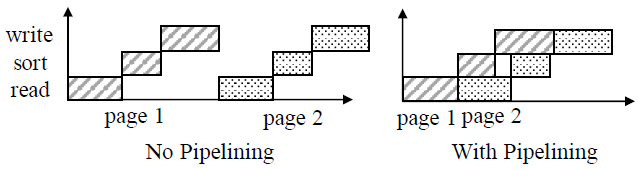
- 如下图所示,将 merge 过程分成三个阶段,使用流水线式实现,从而更好地利用 CPU 和 I/O 并行来提高合并性能
2.2.2. Reducing buffer Cache Misses
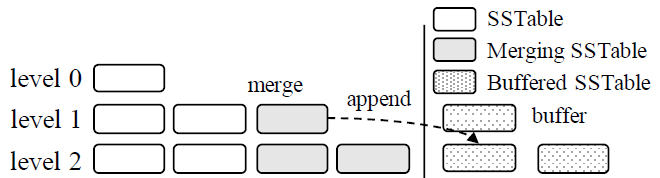
在 merge 操作结束后,由于新的 SSTable 尚未缓存,旧的 SSTables 已被删除,因此查询操作可能因为 cache misses 导致响应耗时增加、性能下降。
2.2.3. Minimizing Write Stalls
3. Representative LSM-based systems
TODO