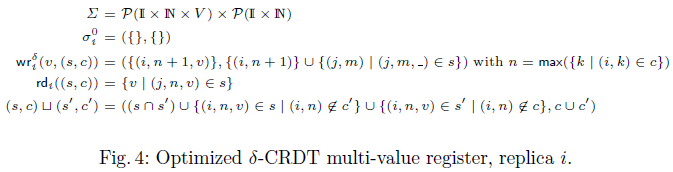《Efficient State-based CRDTs by Delta-Mutation》 阅读笔记。
1. CmRDT 和 CvRDT 的不足
本文作者认为 CmRDT 的不足之处有三:
- 为确保幂等性:要求消息传输提供
exactly once的保证 (本身幂等的操作无需此约束) - 因为两两节点之间都需通信以协调,故动态维护节点之间拓扑结构较为麻烦
- 要求操作在所有节点上单独执行(即使是批量操作)
而 CvRDT 的不足之处则主要在于每次需要传递当前状态,通信消耗过大。
2. Delta-state CRDTs
2.1. Definition
Delta-mutator: A delta-mutator $m^\delta$ is a function, corresponding to an update operation, which takes a state $\mathrm{X}$ in a join-semilattice $\mathrm{S}$ as parameter and returns a delta-mutation $m^\delta(\mathrm{X})$, also in $\mathrm{S}$.
Delta-group: A delta-group is inductively defined as either a delta-mutation or a join of several delta-group.
$\delta$-CRDT: A $\delta$-CRDT consists of a triple $(\mathrm{S}, \mathrm{M}^\delta, \mathrm{Q})$, where $\mathrm{S}$ is a join-semilattice, $\mathrm{M}^\delta$ is a set of delta-mutators, and $\mathrm{Q}$ is a set of query functions, where the state transition at each replica is given by either joining the current state $\mathrm{X} \in \mathrm{S}$ with a delta-mutation:
$$\mathrm{X'} = \mathrm{X} \sqcup m^\delta(\mathrm{X})$$
or joining the current state with some received delta-group $\mathrm{D}$:
$$\mathrm{X'} = \mathrm{X} \sqcup \mathrm{D}$$
2.2. Delta-state decomposition of standards CRDTs
A $\delta$-CRDT $(\mathrm{S}, \mathrm{M}^\delta, \mathrm{Q})$ is a delta-state decomposition of a state-based CRDT $(\mathrm{S}, \mathrm{M}, \mathrm{Q})$, if for every mutator $m \in \mathrm{M}$, we have a corresponding mutator $m^\delta \in \mathrm{M}^\delta$ such that, for every state $\mathrm{X} \in \mathrm{S}$:
$$m(\mathrm{X}) = \mathrm{X} \sqcup m^\delta(\mathrm{X})$$
因此我们的目标便是寻找满足上式的 $m^\delta(\mathrm{X})$,很明显 $m(\mathrm{X})$ 是一个解,因此 CvRDT 是 $\delta$-CRDT 的一种特殊形式。为了克服 CvRDT 通信消耗大的缺点,很明显我们想得到的解需满足以下条件:
$$size(m^\delta(\mathrm{X})) \ll size(m(\mathrm{X}))$$
3. State Convergence
$\delta$-CRDT convergence: Consider a set of replicas of a $\delta$-CRDT object, replica $i$ evolving along a sequence of state $\mathrm{X}^0_i = \perp, \mathrm{X}^1_i$…, each replica performing delta-mutations of the form $m^\delta_{i,k}(\mathrm{X}^k_i)$ at some subset of its sequnece of states, and evolving by joining the current state either with self-generated deltas or with delta-groups received from others. If each delta-mutation $m^\delta(\mathrm{X}^k_i)_{i,k}$ produced at each replica is joined (directly or as part of a delta-group) at least once with every other replica, all replica states become equal.
由 join 操作满足结合律、交换律和幂等易得此结论。
3.1. Basic anti-entropy algorithm

The basic algorithm operators in two modes:
transitivemode: deltas received at node $i$ from node $j$ can later be sent to some other node $k$ (line 21)directmode: a delta-group is exclusively the join of local delta-mutations (line 23)
4. Causal Consistency
在 CvRDT 中每次传输的是 full state,隐式地确保了因果一致性,而在 $\delta$-CRDT 中若想提供因果一致性则需要满足某些条件。
Delta-interval: Given a replica $i$ progressing along the states $\mathrm{X}_i^0, \mathrm{X}_i^1, \dots$ by joining delta $d_i^k$ (either local delta-mutation or recived delta-group) into $\mathrm{X}_i^k$ to obtain $\mathrm{X}_i^{k+1}$, a delta-interval $\Delta_i^{a,b}$ is a delta-group resulting from joining deltas $d_i^a,\dots, d_i^{b-1}$:
$$\Delta_i^{a,b} = \bigsqcup\{d_i^k | a \le k < b\}$$
Delta-interval-based anti-entropy algorithm: A given anti-entropy algorithm for $\delta$-CRDTs is delta-interval-based, if all deltas sent to other replicas are delta-intervals.
Causal delta-merging condition: A delta-interval based anti-entropy algorithm is said to satisfy the causal delta-merging condition if the algorithm only joins $\Delta_j^{a, b}$ from replica $j$ into state $\mathrm{X}_i$ of replica $i$ that satisfy:
$$\mathrm{X}_i \sqsupseteq \mathrm{X}_j^a$$
容易看出上述约束就是通过对消息排序,从而显示地保证因果一致性。也就是说,节点 $j$ 在发送 $\Delta_j^{a,b}$ 之前所 merge 的来自其他节点的 delta-interval 都已被节点 $i$ 所 merge。
$\delta$-CRDT causal consistency: Any $\delta$-CRDT in which states are propagated and joined using a delta-interval-based anti-entropy algorithm satisfying the causal delta-merging condition ensures causal consistency.
也即想要提供因果一致性的保证,basic anti-entropy algorithm 需满足以下约束:
- 是
Delta-interval-based anti-entropy algorithm - 满足
Causal delta-merging condition
CRDT and $\delta$-CRDT correspondence: Let $(\mathrm{S}, \mathrm{M}, \mathrm{Q})$ be sa standard state-based CRDT and $(\mathrm{S}, \mathrm{M}^\delta, \mathrm{Q})$ a corresponding delta-state decomposition. Any $\delta$-CRDT state reachable by an execution $\mathrm{E}^\delta$ over $(\mathrm{S}, \mathrm{M}^\delta, \mathrm{Q})$, by a delta-interval based anto-entropy algorithm $\mathrm{A}^\delta$ satisfying the causal delta-merging condition, is equal to a state resulting from an execution $\mathrm{E}$ over $(\mathrm{S}, \mathrm{M}, \mathrm{Q})$, having the corresponding data-type operations, by an anti-entropy algorithm $A$ for state-based CRDTs.
4.1. Anti-entropy algorithm ensuring causal consistency of $\delta$-CRDT

- Each node $i$ keeps a contiguous sequence of deltas $d_i^l, \dots, d_i^u$ in map $\mathrm{D}$ from integers to deltas, with $l = min(dom(\mathrm{D})), u = max(dom(\mathrm{D}))$.
- Each node $i$ keeps an acknowledgments map $\mathrm{A}$ that stores, for each neighbor $j$, the largest index $b$ for all delta-intervals $\Delta_i^{a,b}$ acknowledged by $j$ (after $j$ receives $\Delta_i^{a,b}$ from $i$ and joins it into $\mathrm{X}_j$)
- 可以看出,在
Algorithm 2中,确保Causal delta-merging condition由发送方完成
推论:Algorithm 2 produces the same reachable states as a standard algorithm over a CRDT for which the $\delta$-CRDT is a decomposition.
5. Examples
5.1. $\delta$-CRDT Counter

- The CRDT state $\Sigma$ is a map from replica identifiers to positive integers
- $inc_i^\delta$ increments the map entry correspondingto the local replica and only returns that entry, instead of the full map as
incin the state-based CRDT counter does.
5.2. $\delta$-CRDTs for Add-Wins OR-Sets

Add-Wins OR-Set with tombstones
- The state $\Sigma$ consists of a set of tagged elements and a set of tags, acting as tombstones
- Globally unique tags of the form $\mathbb{I} \times \mathbb{N}$ are used and ensured by pairing a replica identifier in $\mathbb{I}$ with a monotonically increasing natural counter.
- 在
s中记录添加操作的结果,在t中记录删除操作的结果,两个集合保持单调递增
Optimized Add-Wins OR-Set
- 符号含义和
With Tombstones版本相同 - 维护 causal context set
c而不是 tombstones sett - 在
s中记录此时存在的元素,在c中记录操作历史信息 - 合并操作中,
c可直接join;s在合并之后,保存的是满足以下条件之一的元素- the tripls present in both sets (therefore, not removed in either)
- any triple present in one of the sets and whose tag is not present in the causal context of the other state.
$s \cap s'$ 的存在兼容了传递的信息为 full-state 的情况
Tips: When using an anti-entropy algorithm that provides causal consistency, then for each replica state $\mathrm{X}_i = (s_i, c_i)$ and replica identifier $j \in \mathbb{I}$, we have a contiguous sequence:
$$1 \le n \le max(\{k | (j, k) \in c_i\}) \Rightarrow (j, n) \in c_i$$
因此在消息通信时,通过保证因果一致性,可减少存储空间占用。
5.3. Optimized Multi-value Register $\delta$-CRDT